Plane Table Surveying | Principle | Orientation | Procedure Of Setting Up | Methods

 

PLANE TABLE SURVEYING

 

PRINCIPLE OF PLANE TABLE SURVEYING

The principle of plane tabling is parallelism, meaning that the rays drawn from stations to objects on the paper are parallel to the lines from the stations to the objects on the ground. The relative positions of the objects on the ground are represented by their plotted positions on the paper and lie on the respective rays. The table is always placed at each of the successive stations parallel to the position it occupied at the starting station. Plane tabling is a graphical method of surveying. Here, the fieldwork and plotting are done simultaneously and such survey does not involve the use of a field book.

Plane table survey is mainly suitable for filling interior details when traversing is done by theodolite. Sometimes traversing by a plane table may also be done. But this survey is recommended for work where great accuracy is not required. As the fitting and fixing arrangement of this instrument is not perfect, most accurate work cannot be expected.

 

ACCESSORIES OF A PLANE TABLE

1. The Plane Table

The plane table is a drawing board of 750 mm × 600 mm size made of well-seasoned wood like teak, pine, etc. The top surface of the table is well levelled. The bottom surface consists of a threaded circular plate for fixing the table on the tripod stand by a wing nut.

The plane table is meant for fixing a drawing sheet over it. The positions of the objects are located on this sheet by drawing rays and plotting to any suitable scale (Fig 1).

 

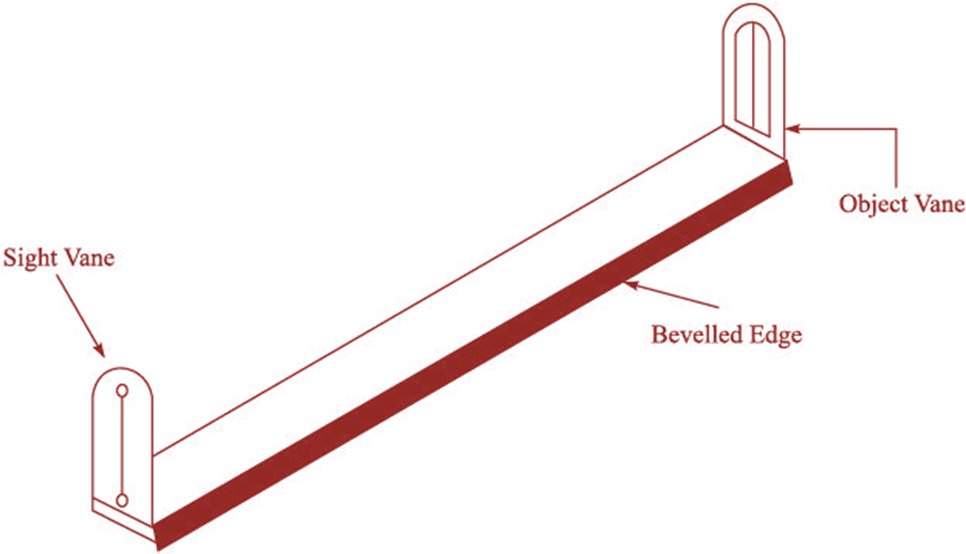
2. The Alidade

There are two types of alidade — plain and telescopic.

(a) Plain Alidade The plain alidade consists of a metal or wooden ruler of length about 50 cm. One of its edges is bevelled and is known as the fiducial edge. It consists of two vanes at both ends which are hinged with the ruler. One is known as the object vane and carries horsehair; the other is called the sight vane and is provided with a narrow slit (fig 2).

 

 

Fig. 1 Plane Table

 

 

Fig. 2 Plane Alidade

 

(b) Telescopic Alidade The telescopic alidade consists of a telescope meant for inclined sight or sighting distant objects clearly. This alidade has no vanes at the ends but is provided with a fiducial edge.

The function of the alidade is to sight objects. The rays should be drawn along the fiducial edge (Fig 3).

 

Fig. 3 Telescopic Alidade

 

3. The Spirit Level

The spirit level is a small metal tube containing a small bubble of spirit. The bubble is visible on the top along a graduated glass tube.

The spirit level is meant for levelling the plane table (fig 4).

 

 

 

Fig. 4 Spirit Level

 

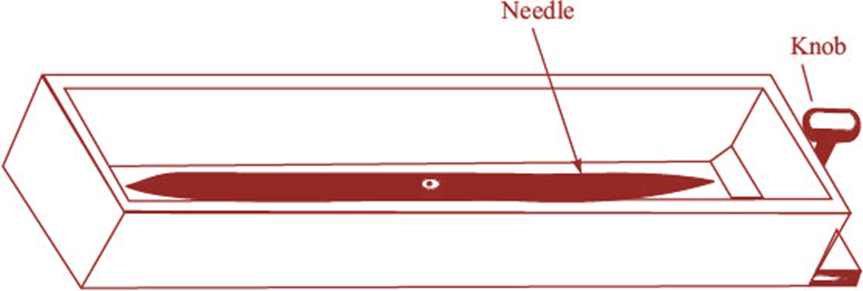
4. The Compass

There are two kinds of compasses — (a) the trough compass, and (b) the circular box compass.

(a) The Trough Compass The trough compass is a rectangular box made of non-magnetic metal containing a magnetic needle pivoted at the centre. This compass consists of a ‘0’ mark at both ends to locate the N-S direction (Fig. 5).

 

Fig. 5 Trough Compass

 

(b) The Circular Box Compass It carries a pivoted magnetic needle at the centre. The circular box is fitted on a square base plate (Fig. 6).

 

Fig. 6 Circular Box Compass

Sometimes two bubble tubes are fixed at right angles to each other on the base plate. The compass is meant for marking the north direction of the map.

 

5. U-fork or Plumbing Fork with Plumb Bob

The U-fork is a metal strip bent in the shape of a ‘U’ (hairpin) having equal arm lengths. The top arm is pointed and the bottom arm carries a hook for suspending a plumb bob (Fig. 7).

 

Fig. 7 U-Fork

 

This is meant for centring the table over a station.

       

 

ORIENTATION OF PLANE TABLE SURVEYING

 

The method of setting up the plane table at each of the successive stations

 

parallel to the position it occupied at the starting station is known as orientation.

Orientation must be done when the plane table is set up at more than one station. As already stated, plane tabling is based on the principle of parallelism. So, the relative positions of the objects on the map will be accurate only if the orientation is proper. But if orientation is not done then the map will not represent the actual positions of the objects.

 

Orientation may be done by magnetic needle and backlighting.

1. Orientation by Magnetic Needle

This method is suitable when the local attraction is not suspected in the area.

Procedure

 

Fig. 8 Orientation by Magnetic Needle

 

(a) Suppose A and B are two stations. The plane table is set up at station A and levelled by a spirit level. The centring is done by U-fork and plumb bob so that point a is just over the station A. Then the trough compass or circular box compass is placed on the right-hand top corner of the sheet in such a way that the needle coincides with ‘0–0’ mark. After this, a line representing the north line is drawn through the edge of the compass box. The table is then clamped.

 

(b) With the alidade touching point A, the ranging rod at B is bisected and a ray is drawn. The distance AB is measured and plotted to any suitable scale.

 

(c) The table is shifted and centred over B so that point b is just over B. The table is levelled. Now the trough compass is placed exactly along the north line drawn previously. The table is then turned clockwise or anticlockwise until the needle coincides exactly with the 0–0 mark of the compass. While turning the table, care should be taken not to disturb the centring. In case it is, it should be adjusted immediately.

(d) When the centring and levelling are perfect and the needle is exactly at 0–0, the orientation is said to be perfect (Fig. 8).

 

2. Orientation by Backsighting

This method is accurate and is always preferred.

Procedure

(a) Suppose A and B are two stations. The plane table is set up over A. The table is levelled by spirit level and centred by U-fork so that point a is just over station A. The north line is marked on the right-hand top corner of the sheet by through compass.

 

(b) With the alidade is touching a the ranging rod at B is bisected and a ray is drawn. The distance AB is measured and plotted to any suitable scale. So, point b represents station B.

 

(c) The table is shifted and set up over B. It is levelled and centred so that b   is just over B. Now the alidade is placed along with the line ba, and the ranging rod at A is bisected by turning the table clockwise or anticlockwise. At this time the centring may be disturbed and should be adjusted immediately if required. When the centring, levelling and bisection of the ranging rod at A are perfect then the orientation is said to be perfect (Fig. 9).

Fig. 9 Orientation by Backsighting

 

PROCEDURE OF SETTING UP A PLANE TABLE OVER A STATION

The following steps have to be performed in order to set up a plane table   over a station:

 

1. Fixing the Table on the Tripod Stand

The tripod stand is placed over the required station with its legs well apart. Then the table is fixed on it by a wing nut at the bottom.

 

2. Levelling the Table

The table is levelled by placing the spirit level at different corners and various positions on the table. The bubble is brought to the centre of its run at every position of the table by adjusting the legs.

 

3. Centring the Table

The drawing sheet is fixed on the table. A suitable point P is selected on the sheet to represent station P on the ground. A pin is then fixed on this selected point. The upper pointed end of the U-fork is made in contact with the station pin and the plumb bob which is suspended from the hook at the lower end is brought just over the station P by turning the table clockwise or anticlockwise or slightly adjusting the legs. This operation is called centring. The table is then clamped. Care should be taken not to disturb the levelling.

 

4. Marking the North Line

The trough compass is placed on the right-hand top corner with its north end approximately towards the north. Then the compass is turned clockwise or anticlockwise so that the needle coincides exactly with the 0–0 mark. Now a line representing the north line is drawn through the edge of the compass. It should be ensured that the table is not turned.

 

5. Orientation

When a plane table survey is to be conducted by connecting several stations,  the orientation must be performed at every successive station.  It may be done by a magnetic needle or by the backsighting method. The backsighting process is always preferred because it is reliable. During orientation, it should always be remembered that the requirements of centring, levelling,  and orientation must be satisfied simultaneously.

 

METHODS OF PLANE TABLING

The following are the four methods of plane tabling:

1. Radiation,

2. Intersection,

3. Traversing, and

4. Resection.

 

1. Radiation

This method is suitable for locating the objects from a single station. In this method, rays are drawn from the station to the objects, and the distances from the station to the objects are measured and plotted to any suitable scale along with the respective rays.

 

Procedure

(a) Suppose P is a station on the ground from where the objects A, B, C and D are visible.

 

(b) The plane table is set up over station P. A drawing sheet is fixed on the table, which is then levelled and centred. A point p is selected on the sheet to represent station P.

 

(c) The north line is marked on the right-hand top corner of the sheet with trough compass or circular box compass.

 

(d) With the alidade touching p, the ranging rods at A, B, C and D  are bisected and the rays are drawn.

 

(e) The distances PA, PB, PC, and PD are measured and plotted to any suitable scale to obtain the points a, b, c, and d, representing the objects  A, B, C and D (Fig. 10), on paper.

 

Fig. 10 Plain Tabling by Radiation

 

2. The Intersection Method

This method is suitable for locating inaccessible points by the intersection of the rays drawn from two instrument stations.

Procedure

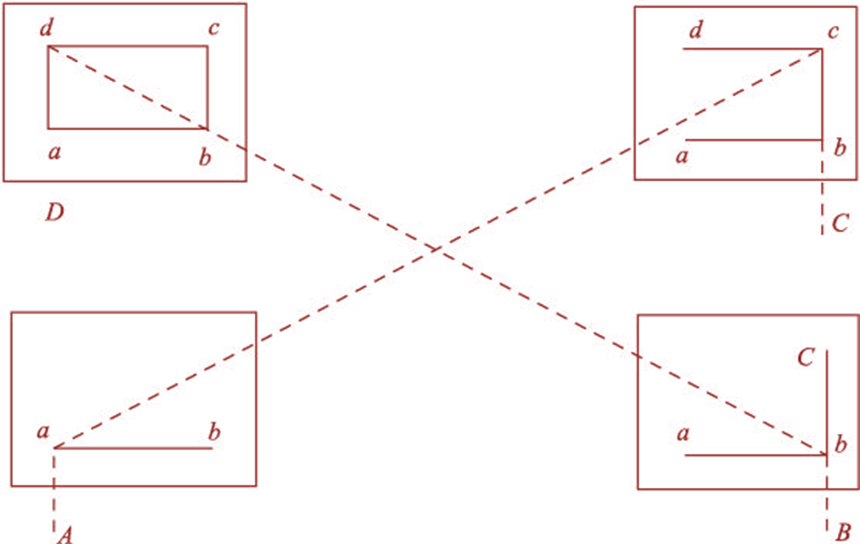
(a) Suppose A and B are two stations and P is an object on the far bank of a river. Now it is required to fix the position of P on the sheet by the intersection of rays, drawn from A and B.

 

(b) The table is set up at A. It is levelled and centred so that a point a on the sheet is just over station A. The north line is marked on the right-hand top corner. The table is then clamped.

 

(c) With the alidade touching an object P and the ranging rod at B are bisected, and rays are drawn through the fiducial edge of the alidade.

 

(d) The distance  AB is measured and plotted to any suitable scale to obtain the point b.

 

(e) The table is shifted and centred over B and levelled properly. Now the alidade is placed along with the line ba and orientation is done by backsighting. At this time, it should be remembered that the centring, levelling and orientation must be perfect simultaneously.

(f) With the alidade is touching b, the object P is bisected and a ray is drawn. Suppose this ray intersects the previous ray at a point p. This point p is the required plotted position of P (Fig. 11).

 

Fig. 11 Plain Tabling by Intersection

 

3. The Traversing Method

This method is suitable for connecting the traverse stations. This is similar to compass traversing or theodolite traversing. But here, fielding and plotting are done simultaneously with the help of the radiation and intersection methods.

 

Procedure

(a) Suppose A, B, C and D are the traverse stations.

 

(b) The table is set up at station A. A suitable point is selected on the sheet in such a way that the whole area may be plotted in the sheet. The table is centred, levelled and clamped. The north line is marked on the right-hand top corner of the sheet.

 

(c) With the alidade touching point a, the ranging rod at B is bisected and a ray is drawn. The distance AB is measured and plotted to any suitable scale.

(d) The table is shifted and centred over B. It is then levelled, oriented by back-sighting and clamped.

 

(e) With the alidade touching the point b, the ranging rod at C is bisected and a ray is drawn. The distance BC is measured and plotted to the same scale.

 

(f) The table is shifted and set up at C and the same procedure is repeated.

 

(g) In this manner, all stations of the traverse are connected.

 

(h) At the end, the finishing point may not coincide with the starting point and there may be some closing error. This error is adjusted graphically by Bowditch’s rule

 

(i) After making the corrections for the closing error, the table is again set up at

 

+ After centring, levelling and orientation, the surrounding details are located by radiation.

 

(j) The table is then shifted and set up at all the stations of the traverse and after proper adjustments, the details are located by the radiation and intersection methods (Fig. 4.12).

 

Fig. 12 Plain Tabling by Traversing

 

4. The Resection Method

This method is suitable for establishing new stations at a place in order to locate missing details.

 

Procedure

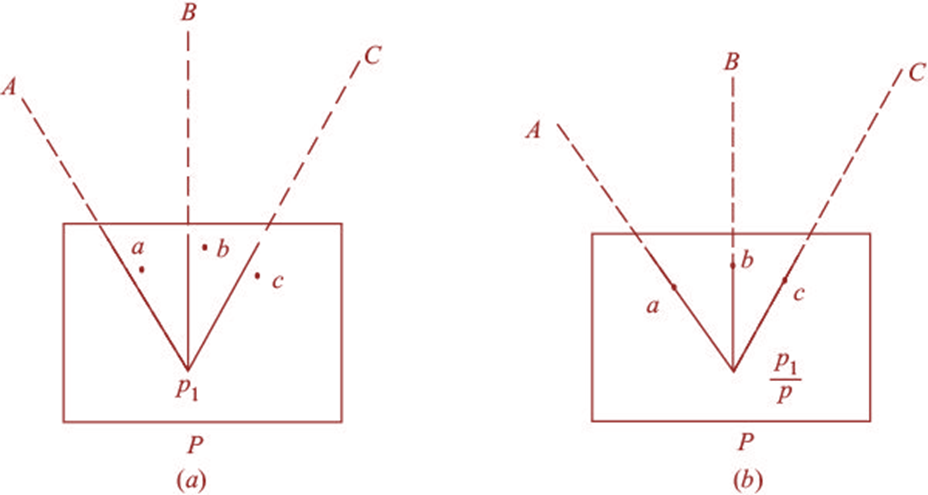
(a) Suppose it is required to establish a station at position P. Let us select two points A and B on the ground. The distance AB is measured and plotted to any suitable scale. This line AB is known as the baseline.

 

(b) The table is set up at A. It is levelled, centred and oriented by bisecting the ranging rod at B. The table. is then clamped.

 

(c) With the alidade touching point a, the ranging rod at P is bisected and a ray is drawn. Then a point P1 is marked on this ray by estimating with the eye.

 

(d) The table is shifted and centred in such a way that P1 is just over P. It is then oriented by backsighting the ranging rod at A.

 

(e) With the alidade touching the point b, the ranging rod at B is bisected and a ray is drawn. Suppose this ray intersects the previous ray at a point P.   This point represents the position of station P on the sheet. Then the actual position of station P is marked on the ground by U-fork and plumb bob (Fig. 13).

 

Fig. 13 Plain Tabling by Resection

 

SPECIAL METHODS OF RESECTION

Sometimes, after the completion of plane table traversing, it may be noticed that an important object has not been located due to oversight. If no station pegs are found on the field, some special methods of resection are applied in order to establish a new station for plotting the missing object. The methods are based on (1) the two-point problem, and (2) the three-point problem.

 

1. The Two-point Problem

In this problem, two well-defined points whose positions have already been plotted on the plan are selected. Then, by perfectly bisecting these points, a new station is established at the required position.

Procedure

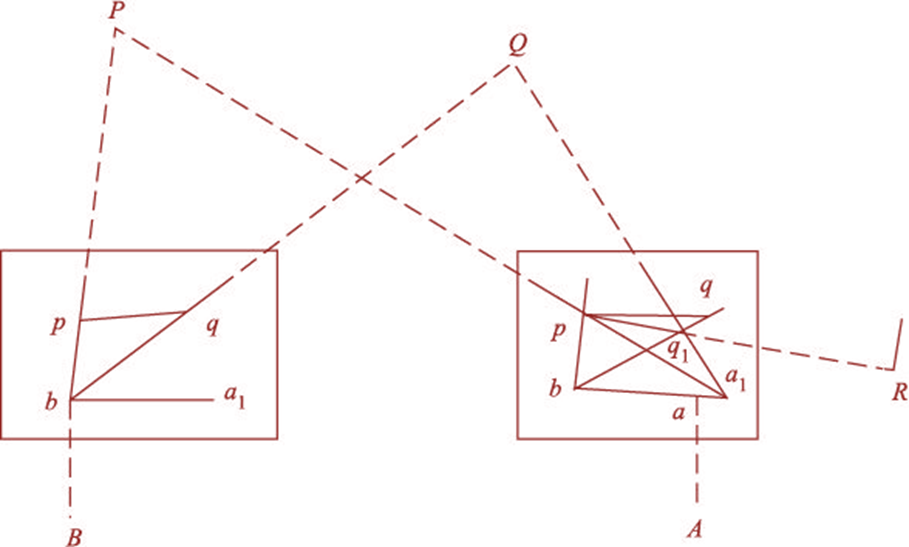
(a) Suppose P and Q are two well-defined points whose positions are plotted on the map as p and q. It is required to locate a new station at A by perfectly bisecting P and Q.

(b) An auxiliary station B is selected at a suitable position. The table is set up at B, and levelled and oriented by eye estimation. It is then clamped.

(c) With the alidade is touching p and q, the points P and Q are bisected and rays are drawn. Suppose these rays intersect at b.

(d) With the alidade centred on b, the ranging rod-at A is bisected and a ray is drawn. Then, by eye estimation, a point a1 is marked on this ray.

(e) The table is shifted and centred on A, with a1 just over A. It is levelled and oriented by backsighting. With the alidade touching p, the point P is bisected and a ray is drawn. Suppose this ray intersects the line ba, at point a1, as was assumed previously.

(f) With the alidade centred on a1, the point Q is bisected and a ray is drawn. Suppose this ray intersects the ray bq at a point q1. The triangle pqq1 is known as the triangle of error and is to be eliminated.

(g) The alidade is placed along the line pq1 and a ranging rod R is fixed at some distance from the table. Then, the alidade is placed along the line PQ and the table is turned to bisect R. At this position, the table is said to be perfectly oriented.

(h) Finally, with the alidade centred on p and q, the points P and Q are bisected and rays are drawn. Suppose these rays intersect at a point a. This would represent the exact position of the required station  A (Fig. 14). Then the station A is marked on the ground.

Fig. 14 Two-point Problem

 

2. The Three-point Problem

In this problem, three well-defined points are selected whose positions have already been plotted on the map. Then, by perfectly bisecting these three well-defined points, a new station is established at the required position.

No auxiliary station is required in order to solve this problem. The table is directly placed at the required position. The problem may be solved by three methods: (a) the graphical or Bessel’s method, (b) the mechanical method,  and (c) the trial-and-error method.

 

(a) The Graphical Method

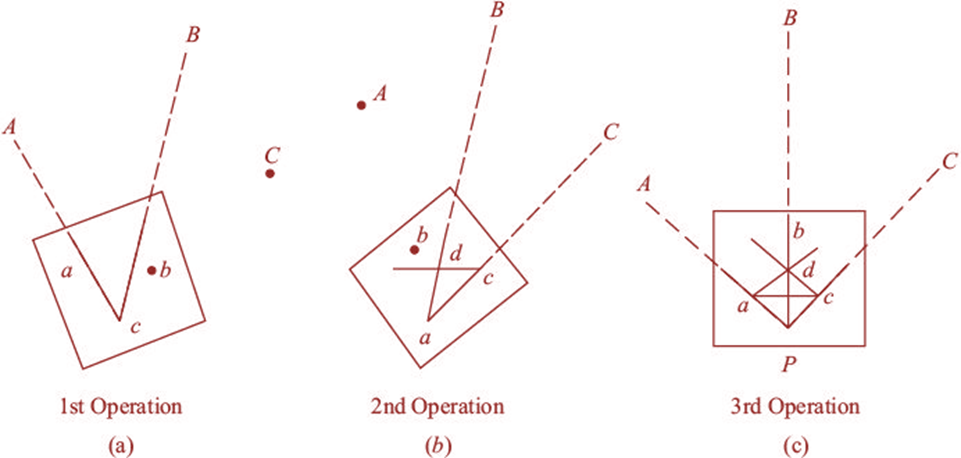
(i) Suppose A, Band C are three well-defined points that have been plotted as a, b, and c. Now it is required to locate a station at P.

 

(ii) The table is placed at the required station P and levelled. The alidade is placed along the line ca and point A is bisected. The table is clamped. With the alidade centred on C, point B is bisected and a ray is drawn   [Fig. 15(a)].

 

(iii) Again the alidade is placed along with the line ac and the point C is bisected and the table is clamped. With the alidade touching a, point  B  is bisected and a ray is drawn. Suppose this ray intersects the previous ray at a point d [Fig. 15(b)].

 

(iv) The alidade is placed along with db and point B is bisected. At this position, the table is said to be perfectly oriented. Now the rays Aa, Bb and Cc are drawn. These three rays must meet at a point p which is the required point on the map. This point is transferred to the ground by a U-fork and plumb bob [Fig. 15(c)].

 

Fig. 15 Solving Three-point Problem Graphically

 

(b) The Mechanical Method

 

(i) Suppose A, B and C are three well-defined points that have been plotted on the map as a, b, and c. It is required to locate a station at P.

 

(ii) The table is placed at P and levelled. A tracing paper is fixed on the map and a point p is marked on it.

 

(iii) With the alidade centred on P, the points A, B and C are bisected and rays are drawn. These rays may not pass through points a, b and c  as the orientation is done approximately [Fig. 16(a)].

 

(iv) Now the tracing paper is unfastened and moved over the map in such a way that the three rays simultaneously pass through the plotted positions a, b, and c. Then the point p is pricked with a pin to give an impression p on the map. p is the required point on the map. The tracing paper is then removed [Fig. 16(b)].

 

(v) Then the alidade is centred on p and the rays are drawn towards A, B and C. These rays must pass through the points a, b and c.

 

Fig. 16 Solving Three-point Problem Mechanically

 

(c) The Method of Trial and Error

 

(a) Suppose A, B and C are three well-defined points that have been plotted as a, b, and c on the map. Now it is required to establish a station at P.

 

(b) The table is set up at P and levelled. Orientation is done by eye estimation.

 

(c) With the alidade, rays Aa, Bb and Cc are drawn. As the orientation is approximate, the rays may not intersect at a point but may form a small triangle—the triangle of error.

 

(d) To get the actual point, this triangle of error is to be eliminated. By repeatedly turning the table clockwise or anticlockwise, the triangle is eliminated in such a way that the rays Aa, Bb, and Cc finally meet at a  point p. This is the required point on the map. This point is transferred to the ground by U-fork and plumb bob (Fig. 17).

 

Fig. 17 Solving Three-point Problem by Trial and Error

READ ALSO: Plane Table Surveying | Errors And Precautions | Procedure | Advantages And Disadvantages

FAQ

1. What is the principle of plane tabling?

The principle of plane tabling is parallelism, meaning that the plane table is always placed in every station parallel to the position it occupied at the first station.

 

2. What is orientation? Why is it done?

The method of keeping the table in successive stations parallel to the position it occupied at the starting station is known as orientation. Orientation is done to perfectly maintain, the relative positions of different objects on the map.

 

3. How are centring and levelling done in plane tabling?

The centring is done by a U-fork and plumb bob. The upper pointed end of the U-fork is kept in contact with the station pin when the plumb bob is just over the station peg.

Levelling is done by a spirit level. The spirit level is placed at the different corners and at various positions on the table. By adjusting the legs of the table, the bubble is brought to the centre.

 

4. What are the methods of plane tabling?

The methods of plane tabling are radiation, intersection, traversing and resection.

 

5. When would you apply resection?

To establish a new station with the help of two points or stations.

 

6. What is the intersection? When is it required?

The method of locating an object by the intersection of rays drawn from two stations is called the intersection method.

This method is applied for locating inaccessible points, which is when it is not possible to measure the distance from the station to the object.

 

7. When would you apply the two-point and three-point problem?

If it is found after completion of the plane table survey that an important object has not been plotted then the two-point or three-point problem is applied to locate a new station. These problems can be applied even if all the station pegs have been removed.

 

8. What do the terms ‘great triangle’ and ‘great circle’ mean?

In the three-point problem, the triangle formed by joining three well-defined points is known as the great triangle and the circle passing through them is called the great circle.

If you find 

This information is helpful, please share it.

 

Thanks! For reading the article...