LENGTH AND AREA CALCULATIONS | IMPORTANT SURFACE AREA FORMULAS | LCETED

LENGTH AND AREA CALCULATIONS

IMPORTANT SURFACE AREA FORMULAS

 

Formulas:

1. Square or Rectangle

(i) Area = A = L x B

(ii) Peripheral Length = L = (L+B) x 2

 

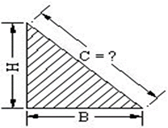
2. Pythagoras theorem

This theorem is used to find out any inclined length

c² = a² +b²

c = Ѵ(a² + b²)

 

3. Tri‐angle

(i) Area = A = 1/2 x B x H

(ii) Peripheral Length = L = B + H + C

 

4. Irregular Tri‐angle

(i) Area = A = Ѵ (s(s‐a) (s‐b) (s‐c))

Where, s = (a + b + c )/2

(ii) Peripheral Length = L = a + b + c

 

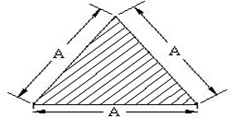
5. Equilateral Tri‐angle

(i) Area = A = (a ²/4) x Ѵ3

(ii) Peripheral Length = L = a + a + a = 3a

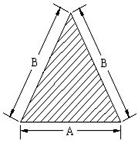
6. Isosceles Tri‐angle

(i) Area = A = (a/4) x Ѵ 4b²‐a²

(ii) Peripheral Length = L = a + b + b = a + 2b

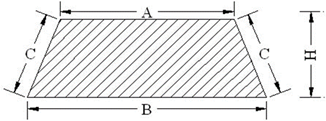
7. Trapezoidal

(i) Area = A = 1/2 ( a+ b) x h

(ii) Peripheral Length = L = a + b + c + c

 

8. Hexagon

(i) Area = A = (0.5 x r x 0.5 x r x Tan60) x 6

(ii) Peripheral Length = L = 6r

9. Circle

(i) Area = A = π/4 x d²

Where, d = diameter of circle ;        π = 3.14

 

(ii) Peripheral Length = L = 2 x π x r

Where, r = radius of circle

 

10. Semi‐Circle

(i) Area = A = π/4 x d² x 0.50

Where, d = diameter of circle ;        π = 3.14

(ii) Peripheral Length = L = 2 x π x r x 0.50 where r = radius of circle

 

11. Quarter Circle

(i) Area = A = π/4 x d² x 0.25

Where, d = diameter of circle ;        π = 3.14

(ii) Peripheral Length = L = 2 x π x r x 0.25 where r = radius of circle

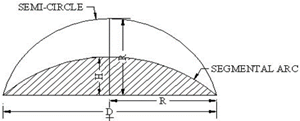
12. Segmental Arc

(i) Area = A = (2/3 x D xH) + (H³/2D)

Where, d = diameter of circle H = height of arc

(ii) Arc Length = L = (8b ‐ 2r)/3

Where, r = radius of circle

b = Ѵ (r² +h²)

If you find 

This information is helpful, please share it.

 

Thanks! For reading the article...